Ghostwriting-Service Dr. Rainer Hastedt
Erfolgsmessung im Marketing - Folge 17: Korrelationsanalysen bitte mit Vorsicht genießen
Dass nicht jede Korrelation auf einen Kausalzusammenhang hindeutet, versteht sich von selbst. Als klassisches Beispiel gilt die positive Korrelation zwischen der Anzahl der Storchenpaare und der in einem Jahr geborenen Kinder. Kausalität würde hier bedeuten, dass Sie durch die Ansiedlung zusätzlicher Storchenpaare die Geburtenrate erhöhen könnten.
Für praktische Anwendungen bringen solche Extremfälle leider nichts, weil bei praktischen Anwendungen so gut wie immer nur Zusammenhänge von Interesse sind, für die sich mehr oder weniger plausible Erklärungen finden.
Stellen Sie sich zum Beispiel vor, Sie investieren jeden Monat viel Geld in Fernsehwerbung. Nach einiger Zeit finden Sie anhand Ihrer Daten eine positive Korrelation zwischen den Aufwendungen für Ihre Fernsehwerbung und dem Umsatz mit den betreffenden Produkten.
Wie deuten Sie diesen Befund?
- »Unsere Fernsehwerbung ist erfolgreich; je mehr wir dafür aufgewendet haben, desto größer war der Umsatz. Wir sollten daher mehr Fernsehwerbung buchen und dadurch unseren Umsatz weiter erhöhen (Kausalität).«
- »Die Korrelation besagt nichts, weil unser Umsatz auch von anderen Faktoren beeinflusst wurde, unter anderem von unseren Promotions, von unserer Preispolitik und der positiven Entwicklung der Marktnachfrage.«
Beide Sichtweisen sind diskussionswürdig, da Sie Kausalität auch stochastisch interpretieren können: Wenn Sie mehr Fernsehwerbung buchen, dann wird Ihr Umsatz mit hoher Wahrscheinlichkeit steigen. Gelegentliche Rückschläge (mehr Fernsehwerbung und trotzdem weniger Umsatz) wären demnach mit dem Bestehen eines Kausalzusammenhangs vereinbar.
Wie Sie anhand des Beispiels sehen, sind inhaltliche Überlegungen manchmal zu wenig, um die Frage »Kausalität ja oder nein?« eindeutig beantworten zu können.
Hilfreich sind daher statistische Verfahren, mit denen Sie gegebenenfalls Hinweise auf einen fehlenden Kausalzusammenhang erhalten.
Ich will dies anhand eines Zahlenbeispiels erläutern.
Ein Random-Walk mit Excel
Sie sehen in der folgenden Excel-Tabelle Daten für die Variablen X und Y, die ich mit Hilfe von Zufallszahlen erzeugt habe.
Die Zufallszahlen stellen sicher, dass X und Y voneinander unabhängig sind und Kausalität daher verneint werden muss. Ich kann dann prüfen, wodurch sich die fehlende Kausalität bemerkbar macht.
Ich habe die Excel-Tabelle wie folgt erstellt:
1. Die Werte in den Zellen A2 bis A32 stehen für die Perioden (zum Beispiel Monate), auf die sich meine Daten beziehen. Ich habe die Zahlen 1 bis 31 mit dem Dialog Start / Füllbereich / Reihe eingefügt.
2. In den Spalten B und C stehen meine Zufallszahlen, die ich mit dem Analyse-Toolpack erzeugt habe: Dialog Daten / Datenanalyse / Zufallszahlengenerierung mit den Einstellungen Verteilung: »Gleichverteilt«, Parameter zwischen 0 und 1, Ausgabebereich: B2:C32, die übrigen Eingabefelder ignorieren, mit OK bestätigen.
Anschließend habe ich die Darstellung der Zufallszahlen geändert: B2:C32 mit der Maus markieren, die rechte Maustaste drücken, Menüpunkt Zellen formatieren / Zahlen, Kategorie Zahl, sechs Dezimalstellen. Die anderen Zahlenwerte habe ich auf die gleiche Weise formatiert.
3. In Zelle D2 habe ich den willkürlich gewählten Wert 1 eingetragen. Der Wert in Zelle D3 ergibt sich durch die Formel =D2+B3. Die Zellen D4 bis D32 habe ich durch Ziehen mit der Maus ausgefüllt. Aus einem X-Wert entsteht somit durch Addition einer Zufallszahl aus Spalte B ein neuer X-Wert.
4. Für die Variable Y habe ich in Zelle E2 den Wert 20 gewählt. Der Wert in Zelle E3 ergibt sich durch die Formel =E2+(1,5-2*C3)*C3. Wichtig ist hier, dass ich die Zufallszahlen aus Spalte C verwende (und nicht aus Spalte B, mit der ich die X-Werte konstruiert habe). Auch hier habe ich die Formel durch Ziehen mit der Maus in die übrigen Zellen übertragen.
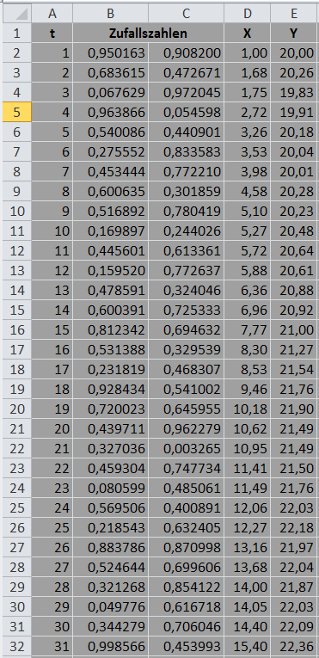
Mit der Formel =PEARSON(D2:D32;E2:E32) erhalte ich einen Korrelationskoeffizienten in Höhe von 0,96. Zwischen den Variablen X und Y besteht demnach eine sehr stark ausgeprägte positive Korrelation.
Ein zweiseitiger Signifikanztest ergibt die Werte t = 19,7495 und p = 0,000 (ich habe hierfür eines meiner Excel-Templates verwendet). Die beobachtete Korrelation ist somit statistisch hochsignifikant.
Ich halte fest:
Zwischen den Variablen X und Y besteht eine statistisch hochsignifikante sehr stark ausgeprägte positive Korrelation - obwohl beide Variablen voneinander unabhängig sind und daher Kausalität ausgeschlossen ist.
Durch die Korrelationsanalyse wird somit ein Ursache-Wirkungs-Zusammenhang suggeriert, wo keiner sein kann. Bislang ist dies nur klar, weil Sie wissen, wie ich meine Daten konstruiert habe.
Einfache lineare Regression
Der mit Excel berechnete Pearson-Korrelationskoeffizient misst die Stärke des linearen Zusammenhangs zwischen den Variablen X und Y. Ich untersuche meine Daten daher anhand einer linearen Regressionsanalyse.
Ich habe die X- und Y-Werte zunächst in Excel als Punktdiagramm dargestellt. Anschließend habe ich das Diagramm mit der Maus ausgewählt, den Dialog Layout / Trendlinie / Weitere Trendlinienoptionen geöffnet und hier die Optionen »Linear« und »Formel im Diagramm anzeigen« gewählt:
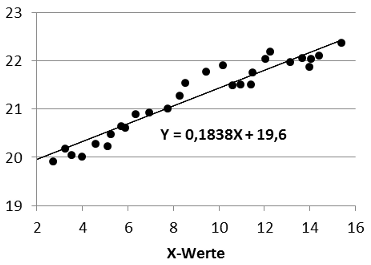
Wie Sie sehen, beschreibt die Regressionsgerade Y = 0,1838X + 19,6 die eingezeichneten Datenpunkte sehr gut.
Ich will die Regressionsgerade jetzt mit statistischen Methoden prüfen. Hierzu öffne ich in Excel den Dialog Daten / Datenanalyse / Regression, lege zunächst fest, wo Excel die Daten ausgeben soll, wähle als Y-Eingabebereich E2:E32, als X-Eingabebereich D2:D32, markiere das Feld »Residuen« und bestätige mit OK.
Nach den von Excel berechneten Kennzahlen macht die Regressionsgerade einen sehr guten Eindruck. Beide Koeffizienten sind hochsignifikant (jeweils p = 0,000) mit relativ kleinen 0,95-Konfidenzintervallen (0,1838±0,019 und 19,6±0,1766).
Es fehlt allerdings der Durbin-Watson-Koeffizient, den ich anhand der von Excel ausgegebenen Residuen berechnen kann. Der Durbin-Watson-Koeffizient sollte bei 2 liegen.
Wenn die Residuen in den Zellen F2 bis F32 stehen, dann ergibt sich der Durbin-Watson-Koeffizient aus der Berechnungsformel =SUMMEXMY2(F3:F32; F2:F31)/QUADRATESUMME(F2:F32). Auf diese Weise erhalte ich DW = 0,79 und komme daher zu dem Ergebnis, dass das durch die Regressionsgerade beschriebene Modell unbrauchbar sein könnte.
Modelldiagnostik: Autokorrelation
Das im obigen Diagramm dargestellte Modell beschreibt eine Kausalbeziehung im stochastischen Sinne:
Sie geben einen X-Wert vor und erhalten durch die Regressionsgleichung den zugehörigen Funktionswert 0,1838X + 19,6 und damit den zu erwartenden Y-Wert. Der sich tatsächlich ergebende Y-Wert kann hiervon abweichen, weil auch andere Faktoren eine Rolle spielen. Die sich tatsächlich ergebenden Y-Werte liegen daher nur selten auf der Regressionsgeraden.
Wenn das Modell korrekt spezifiziert ist, dann hat nur die Variable X einen systematischen Einfluss auf die Variable Y. Systematisch heißt, dass der Einfluss von X mit Hilfe einer Regressionsgleichung beziffert werden kann. Die als Residuen bezeichneten vertikalen Abweichungen der Datenpunkte von der Regressionsgeraden sind im Fall eines korrekt spezifizierten Modells unsystematisch.
Autokorrelation liegt vor, wenn die Residuen miteinander korreliert sind und daher einem bestimmten System folgen. Das Modell wäre dann unbrauchbar.
Der mit Excel berechnete Wert DW = 0,79 deutet hierauf hin.
Ich muss das Modell daher auf Autokorrelation testen. Weil Excel derartige Tests nicht unterstützt, nutze ich R (Näheres zu R auf meiner Seite Statistik-Service).
Ich lese zunächst meine Daten, die sich bei mir in der Datei 0018.xlsx befinden (Worksheet 3, Zeilen 1 bis 32 von Spalte 1 bis 5). Ich gebe den in R eingelesenen Daten den Namen »daten«.
library(xlsx)
daten <- read.xlsx("0018.xlsx", sheetIndex=3, colIndex=1:5, rowIndex=1:32)
Dann kommt meine Regressionsanalyse, die ich »reg« nenne:
reg <- lm(Y~X, data=daten)
Ich beginne mit dem Durbin-Watson-Test, rechne dann einen Breusch-Godfrey Test auf Autokorrelation 1. Ordnung mit Chi-Quadrat-Verteilung und schließlich einen Ljung-Box-Test, ebenfalls auf Autokorrelation 1. Ordnung:
library(lmtest)
dwtest(reg, alternative="two.sided")
bgtest(reg)
Box.test(residuals(reg), type="Ljung-Box")
Die sich hierbei ergebenden Signifikanzniveaus sind p=0,000 (Durbin-Watson), p=0,001 (Breusch-Godfrey) und p=0,001 (Ljung-Box).
Ich muss daher die Nullhypothese »Residuen ohne Autokorrelation 1. Ordnung« ablehnen.
Mein Modell Y = 0,1838X + 19,6 ist demnach unbrauchbar.
Autokorrelation kann unter anderem auch deshalb auftreten, weil die gewählte Regressionsgleichung die falsche Form hat. Sie haben zum Beispiel Daten, die einen u-förmigen Zusammenhang nahelegen und versuchen Ihre Daten trotzdem durch eine Gerade zu beschreiben.
Ich prüfe daher, ob die gewählte Kurvenform angemessen ist. Hierzu zeichne ich zunächst einen Marginal Model Plot:
png("emim-17-2.png", width=370, height=240, bg="transparent")
library(ggplot2)
ggplot(data=daten, aes(x=X, y=Y)) + geom_point() + theme_bw() + xlab("X-Werte") + ylab("") + theme(plot.background = element_rect(colour=NA, fill="transparent")) + geom_smooth(method="lm", se=FALSE, colour="red") + geom_smooth(method="loess", se=FALSE)
dev.off()
Sie sehen jetzt die Regressionsgerade (rot) und zusätzlich eine LOESS-Linie (blau), die deutlich von der Regressionsgeraden abweicht:
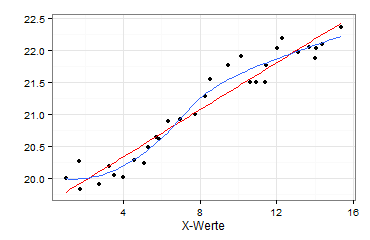
Wegen dieser Abweichung teste ich, ob die gewählte Funktionsform Y = a + bX korrekt ist. Sinnvoll sind hier vor allem ein Harvey-Collier-Test und ein Rainbow-Test:
harvtest(reg)
raintest(reg)Als Signifikanzniveaus erhalte ich p=0,598 (Harvey-Collier) und p=0,519 (Rainbow). Die gewählte Funktionsform Y = a + bX ist demnach in Ordnung.
Konsequenzen
Meine Frage:
Kann ich die stark ausgeprägte Korrelation zwischen den Variablen X und Y als Kausalbeziehung deuten?
Wenn ich die Frage bejahe, dann sage ich, dass ich die Variable X als Steuergröße ansehe, mit der ich das Niveau von Y beeinflussen kann. Ich erhöhe zum Beispiel X um fünf Prozent und kann im Fall eines Kausalzusammenhangs abschätzen, wie sich dies voraussichtlich auf Y auswirken wird.
Der berechnete Korrelationskoeffizient r=0,96 misst die Stärke des linearen Zusammenhangs zwischen den Variablen X und Y. Das Ergebnis r=0,96 macht daher nur Sinn, wenn sich die Beziehung zwischen X und Y durch eine Funktion vom Typ Y = a + bX beschreiben lässt.
Meine Tests sprechen für einen linearen Zusammenhang zwischen den Variablen X und Y. Der Pearson-Korrelationskoeffizient r=0,96 ist daher für meine Daten aussagekräftig.
Die gefundene Regressionsgleichung Y = 19,6 + 0,1838X hat sich trotzdem als unbrauchbar erwiesen (Autokorrelation). Aus diesem Grund sind auch die Signifikanztests für die Koeffizienten dieser Regressionsgleichung unbrauchbar (Modellannahmen für die Residuen verletzt).
Die positive Korrelation zwischen X und Y ist somit kein Kausalzusammenhang.
Zwischen den Variablen X und Y kann trotz meines negativen Ergebnisses eine andere Form des Kausalzusammenhangs bestehen.
Die diagnostizierte Autokorrelation kann daran liegen, dass in der Regressionsgleichung bedeutende Variablen fehlen, nicht Y = a + bX, sondern vielleicht Y = b0 + b1X + b2X2 + b3X3. Ein solches Modell müsste ich erneut prüfen.
Internetseiten
Fachbeiträge
Das liberale Propaganda-Handbuch, Taschenbuch, 382 Seiten
Einführung in die Statistik-Software R Commander
Business Cases für den Verkauf
Fachliteratur suchen mit Google Scholar, WorldCat etc. pp.
Ghostwriter für Dissertationen, Bachelor- und Masterarbeiten
Wissenschaftliches Ghostwriting
Content-Marketing mit White Papers für Start-up-Unternehmen im B2B-Geschäft
1. White Papers als Werbemittel
2. Fallstudien im Sinne von White Papers
Warum White Papers im B2B-Geschäft häufig wirkungsvoller sind als klassische Werbung
Lead-Management im B2B-Geschäft - warum und wie?
White Papers erstellen - von der Themenwahl bis zum Layout