Ghostwriting-Service Dr. Rainer Hastedt
Erfolgsmessung im Marketing - Folge 8: Lohnt sich Kundenbindung?
Unternehmensberater empfehlen ihren Klienten häufig Maßnahmen zur Verbesserung der Kundenbindung. Dies soll vorteilhaft sein, weil die Akquisition von Neukunden relativ teuer ist und sich daher anbietet, einen höheren Umsatz mit den bereits vorhandenen Kunden anzustreben.
Der Schwachpunkt derartiger Ratschläge liegt in ihrem pauschalen Charakter: Auch Kundenbindung verursacht Kosten.
Kundenbindungsprogramme sind nur sinnvoll, wenn sie sich - voraussichtlich - positiv auf den Unternehmensgewinn auswirken. Der Verweis auf hohe Akquisitionskosten ist daher ein Scheinargument.
Ich beschäftige mich aus diesem Grund mit der Frage, wie Sie anhand von Daten aus dem betrieblichen Rechnungswesen beurteilen können, ob Investitionen der genannten Art vorteilhaft sind oder nicht.
Grundsätzliches zur Vorgehensweise
Im Mittelpunkt der folgenden ROI-Analyse steht die Kundenbindungsrate, die in Form eines Prozentsatzes angibt, wie viele Ihrer derzeitigen Kunden auch in der folgenden Periode bei Ihnen kaufen.
Eine Kundenbindungsrate in Höhe von 80 Prozent bedeutet somit, dass 80 von 100 aktuellen Kunden auch in der nächsten Periode zu Ihren Kunden gehören.
Sie sehen anhand der Kundenbindungsrate, wie viele Kunden Sie von Periode zu Periode verlieren. Im Zahlenbeispiel sind dies 20 Prozent (1 - Kundenbindungsrate).
Die Kundenbindungsrate eignet sich nicht, die durchschnittliche Dauer von Kundenbeziehungen zu schätzen. Der verlockende Ansatz
Durchschnittliche Dauer = 1 / (1 - Kundenbindungsrate)
würde im Zahlenbeispiel auf eine durchschnittliche Kundenlebensdauer von fünf Jahren hinauslaufen; 5 = 1/(1-0,8).
Eine solche Vorgehensweise ist unzureichend, weil Sie in diesem Fall damit rechnen müssen, dass Sie den Kundenwert CLV stark überschätzen (Sunil Gupta und andere: Modeling Customer Lifetime Value, Journal of Service Research, November 2006, S. 141).
Dies erklärt, warum ich bei meiner ROI-Analyse auf eine Schätzung der durchschnittlichen Kundenlebensdauer verzichte und stattdessen eine etwas aufwändigere Vorgehensweise bevorzuge.
Die Ausgangsdaten
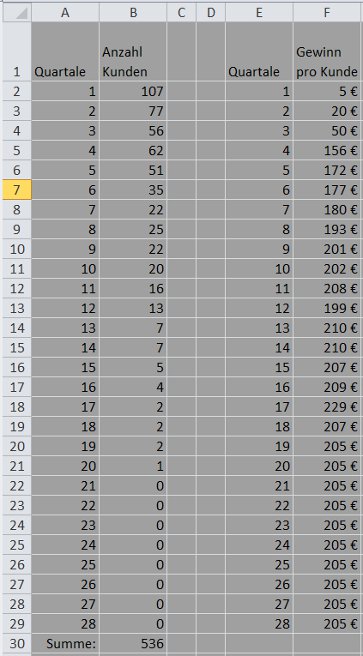
Sie sehen in der linken Hälfte der folgenden Tabelle Daten über die Dauer der Geschäftsbeziehung mit 536 ehemaligen Kunden. 107 Kunden hatten die Geschäftsbeziehung bereits nach einem Quartal beendet, 77 nach zwei Quartalen und einer dieser Kunden erst nach 20 Quartalen, nach fünf Jahren.
Die von mir gewählte Zeiteinteilung (Quartale) ist als Beispiel zu verstehen. Es kann sein, dass eine andere Zeiteinteilung besser zu Ihren Daten passt.
In der rechten Hälfte der folgenden Tabelle sehen Sie den durchschnittlichen Quartalsgewinn pro Kunde, gestaffelt nach der Dauer der Geschäftsbeziehung. Die Daten zum durchschnittlichen Quartalsgewinn pro Kunde sollten möglichst aktuell sein und müssen daher nicht unbedingt von den Kunden stammen, die in der linken Tabellenhälfte berücksichtigt sind.
Die rechte Tabellenhälfte besagt:
Im ersten Quartal der Geschäftsbeziehung beträgt der durchschnittliche Quartalsgewinn pro Kunde 5 Euro, im zweiten Quartal der Geschäftsbeziehung erhöht sich der durchschnittliche Quartalsgewinn pro Kunde auf 20 Euro und im dritten Quartal auf 50 Euro.
Im nächsten Schritt habe ich die Kundenbindungsrate geschätzt. Ich habe hierzu so gerechnet, als ob sämtliche Geschäftsbeziehungen zu Beginn des ersten Quartals begründet wurden.
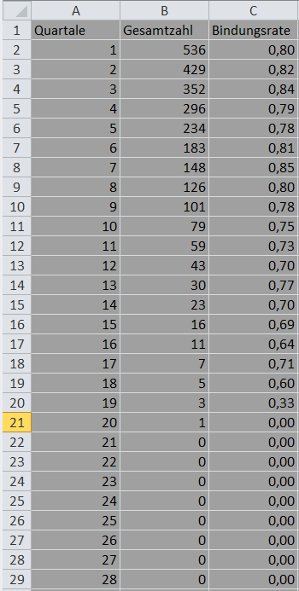
In Quartal 1 hat das Unternehmen 536 Kunden (Zelle B2 der folgenden Tabelle). In Quartal 2 sind hiervon nur noch 429 übrig (536-107 = 429). In Quartal 3 sind von den 429 Kunden nur noch 352 übrig (429-77 = 352).
Spalte C der folgenden Tabelle enthält die Werte der Kundenbindungsrate. Die Zahl in Zelle C2 ergibt sich aus der Formel =B3/B2 (0,80 = 429/536; auf zwei Stellen gerundet mit dem Dialog Zellen formatieren / Zahlen / Zahl).
Weil Excel nicht durch Null dividieren kann, habe ich die Berechnungsformel für die Kundenbindungsrate modifiziert: =WENN(B2=0; 0; B3/B2). Excel prüft demnach zuerst, ob durch Null dividiert werden müsste. Wenn dies zutrifft, setzt Excel die Kundenbindungsrate gleich Null. Andernfalls berechnet Excel den Wert B3/B2.
Der Kundenwert CLV
Aufgrund des vorherigen Abschnitts haben Sie Schätzwerte für den durchschnittlichen Quartalsgewinn pro Kunde und die Kundenbindungsrate.
Sie können jetzt für eine beliebige Kundengruppe den Kundenwert ΣCLV schätzen (Summe aller individuellen Kundenwerte CLV).
Ich betrachte eine Gruppe von 500 Kunden im Zeitraum vom 1. Februar 2012 bis zum 31. Januar 2019:
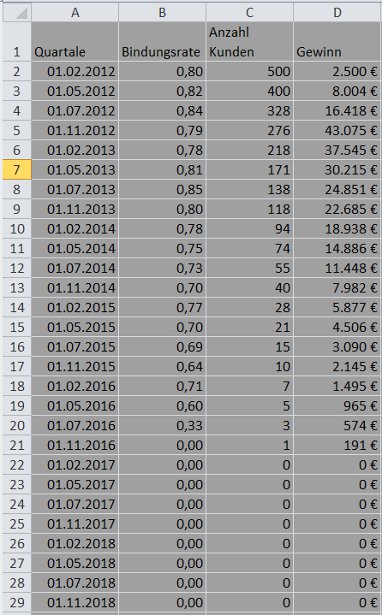
In Spalte A sehen Sie die Zeiteinteilung. Das erste Quartal beginnt am 1. Februar 2012 und endet am 30. April 2012.
Spalte B enthält die Schätzwerte für die Kundenbindungsrate.
Der Wert in Zelle C2 (500) ist vorgegeben. Die übrigen Werte (C3 bis C29) ergeben sich durch Multiplikation der bisherigen Kundenzahl mit der Kundenbindungsrate. Für Zelle C3 lautet die Berechnungsformel daher =B2*C2. Das Ergebnis 400 ist gerundet mit dem Dialog Zellen formatieren / Zahlen / Zahl.
In Spalte D habe ich den jeweiligen Quartalsgewinn berechnet. Der Ansatz lautet: Kundenzahl mal durchschnittlicher Quartalsgewinn pro Kunde, für das erste Quartal 500 Kunden mal 5 Euro pro Kunde = 2.500 Euro.
Den Kundenwert aller 500 Kunden berechne ich nach der Formel =XKAPITALWERT(0,1; D2:D29; A2:A29). Der Wert 0,1 ist mein Kalkulationszinssatz. In den Zellen D2 bis D29 stehen die Quartalsgewinne, die abgezinst und summiert werden sollen. Die Zellen A2 bis A29 beschreiben die Zeiteinteilung.
Das Ergebnis (ΣCLV) ist gleich 224.586,94 Euro. Die 500 Kunden haben demnach einen Kundenwert in Höhe von insgesamt 224.586,94 Euro (Annahme: Kalkulationszinssatz = 10 Prozent).
Ich hatte den Kundenwert in Folge 3 mit der NBW-Funktion berechnet. Dies war möglich, weil ich die Zeit im dort verwendeten Zahlenbeispiel in Jahre eingeteilt hatte.
Die XKAPITALWERT-Funktion unterscheidet sich von der NBW-Funktion im Prinzip nur dadurch, dass die Zeiteinteilung zunächst in Jahre umgerechnet wird. Sie sehen dies, wenn Sie den Kundenwert der 500 Kunden ohne die XKAPITALWERT-Funktion berechnen:
In Spalte B der folgenden Tabelle habe ich berechnet, wie viele Jahre der jeweilige Quartalsbeginn vom 1. Februar 2012 entfernt ist. Ich habe hierbei berücksichtigt, dass Excel Datumsangaben als Zahlen speichert. Daher ergibt sich der Wert in Zelle B3 aus der Formel =(A3-A2)/365 oder =(A3-$A$2)/365. (Die zweite Variante ist besser, weil Sie bei dieser Schreibweise die Zellen B4 bis B29 durch Ziehen mit der Maus ausfüllen können.)
In Spalte C der folgenden Tabelle finden Sie die Abzinsungsfaktoren. Der Wert in Zelle C2 ist gleich eins, weil das erste Quartal als Gegenwartsperiode fungiert. Alle später entstehenden Gewinne werden dagegen abgezinst, im Beispiel mit einem Kalkulationszinssatz in Höhe von zehn Prozent.
Der Abzinsungsfaktor für das zweite Quartal (Zelle C3) ergibt sich somit aus der Formel =1/(1+0,1)^B3. Für das dritte Quartal (Zelle C4) lautet die Formel =1/(1+0,1)^B4. (Hinweise zu den Abzinsungsfaktoren finden Sie in Folge 3 meiner Serie »Erfolgsmessung im Marketing«.)
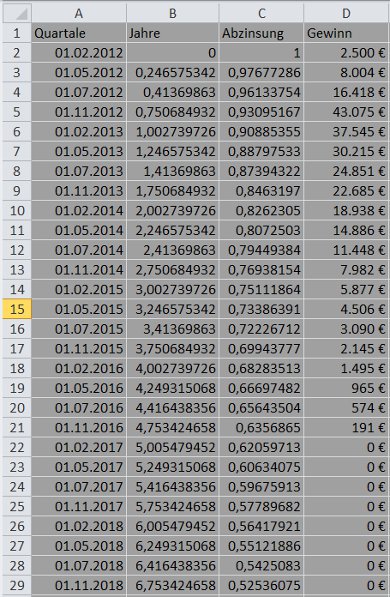
Ich muss jetzt nur noch die Quartalsgewinne (Spalte D) mit den entsprechenden Abzinsungsfaktoren (Spalte C) multiplizieren und die Ergebnisse addieren. Die Formel lautet =SUMMENPRODUKT(D2:D29; C2:C29).
Das Ergebnis - der Kundenwert aller 500 Kunden (ΣCLV) - ist wieder gleich 224.586,94 Euro.
Was-wäre-wenn-Analyse
Ich beschäftige mich jetzt mit der Frage, wie sich Änderungen der Kundenbindungsrate auf den Kundenwert einer Kundengruppe auswirken. Excel bietet hierzu die Option Daten / Was-wäre-wenn-Analyse / Datentabelle.
Betrachten Sie das folgende Arbeitsblatt:
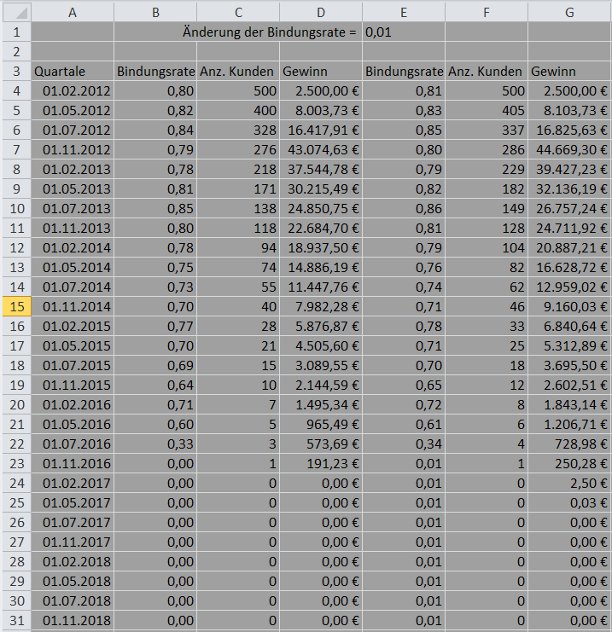
Die Daten in den Spalten A, B, C und D der obigen Tabelle kennen Sie bereits aus dem vorherigen Abschnitt.
Zelle E1 enthält den Wert für die Änderung der Kundenbindungsrate, den ich mit 0,01 angesetzt habe. In Zelle E4 bis E31 sehen Sie die entsprechend geänderten Kundenbindungsraten. Der Wert in Zelle E4 ergibt sich demnach aus der Formel =B4+$E$1, wobei das Ergebnis wieder auf zwei Stellen gerundet ist (mit dem Dialog Zellen formatieren / Zahlen / Zahl).
In den Spalten F und G habe ich berechnet, wie sich die veränderte Kundenbindungsrate auf die Kundenzahl und den Quartalsgewinn auswirkt. (Das Berechnungsverfahren finden Sie im vorherigen Abschnitt »Der Kundenwert CLV«.)
Die Frage lautet:
Wie beeinflusst eine Änderung der Kundenbindungsrate den Kundenwert der betrachteten Kundengruppe?
Eine Antwort finden Sie in der folgenden Wertetabelle, die in Spalte A unterschiedliche Werte für die Veränderung der Kundenbindungsrate enthält und in Spalte B den jeweiligen Kundenwert der Kundengruppe.
In Zeile 44 sehen Sie den Ausgangszustand mit einem Kundenwert in Höhe von insgesamt 224.586,94 Euro. Zeile 45 besagt, dass eine Erhöhung der Kundenbindungsrate um einen Prozentpunkt (+0,01) den Kundenwert der betrachteten Kundengruppe auf 241.097,52 Euro erhöht.
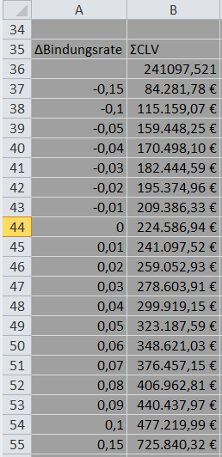
Sie können eine derartige Wertetabelle mit Excel sehr leicht erstellen:
Sie geben zunächst vor, welche Veränderungen der Kundenbindungsrate für Sie interessant sind (A37 bis A55).
Dann schreiben Sie die Berechnungsformel für den Kundenwert der betrachteten Kundengruppe (in Zelle B36 steht die Formel =XKAPITALWERT(0,1; G4:G31; A4:A31), die Sie durch das benutzerdefinierte Zellenformat ;;; unsichtbar machen können).
Zum Abschluss markieren Sie den Bereich A36:B55, gehen zu Daten / Was-wäre-wenn-Analyse / Datentabelle, schreiben in das Feld »Werte aus Spalte« E1 (weil hier die Veränderung der Kundenbindungsrate festgelegt wird) und bestätigen mit OK.
ROI-Analyse
Ich werde jetzt die obige Was-wäre-wenn-Analyse verfeinern. Hierzu berücksichtige ich, dass Sie die Kundenbindungsrate normalerweise nur durch Investitionen erhöhen können, zum Beispiel durch Schulung von Mitarbeitern oder die Einführung eines Kundenbindungsmanagements.
Betrachten Sie die folgende Tabelle, die im Prinzip genauso gemacht ist wie die Tabelle zur Was-wäre-wenn-Analyse aus dem vorherigen Abschnitt:
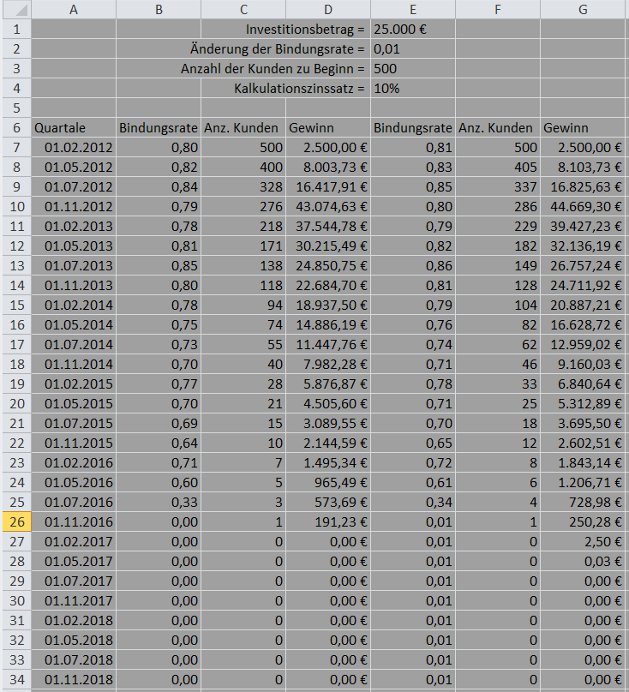
In den Zellen E1 bis E4 setzen Sie die Parameter, den Investitionsbetrag (E1), die hierdurch möglicherweise bewirkte Änderung der Kundenbindungsrate (E2), die Anzahl der Kunden zu Beginn (E3) und den Kalkulationszinssatz, mit dem Sie alle zukünftigen Aufwendungen und Erträge abzinsen (E4).
Die Spalten B, C und D zeigen den Ausgangszustand. Der Wert in Zelle C7 ist durch die Verknüpfung =E3 eingefügt und daher immer mit dem Wert aus Zelle E3 identisch.
Die Spalten E, F und G zeigen, wie sich eine Änderung der Kundenbindungsrate auswirkt. Der Wert in Zelle F7 ist ebenfalls durch die Verknüpfung =E3 eingefügt.
Im Ausgangszustand ergibt sich der Kundenwert der betrachteten Kundengruppe aus der Formel =XKAPITALWERT(E4; D7:D34; A7:A34) mit E4 als Kalkulationszinssatz (0,1).
Im Fall einer erhöhten Kundenbindungsrate ergibt sich der Kundenwert aus der Formel =XKAPITALWERT(E4; G7:G34; A7:A34).
Der Ansatz lautet somit:
Sie investieren einen bestimmten Geldbetrag in die Verbesserung der Kundenbindung (zum Beispiel 25.000 Euro, Zelle E1). Diese Investition bewirkt eine Erhöhung der Kundenbindungsrate (zum Beispiel um einen Prozentpunkt, Zelle E2).
Der Kundenwert der betrachteten Kundengruppe steigt dann um XKAPITALWERT(E4; G7:G34; A7:A34) -XKAPITALWERT(E4; D7:D34; A7:A34). Ich habe diese Differenz in der Formel für den ROI mit ΔΣCLV bezeichnet.
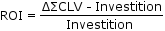
Sie erhalten demnach den ROI, indem Sie von der Differenz XKAPITALWERT(E4; G7:G34; A7:A34) -XKAPITALWERT(E4; D7:D34; A7:A34) den Investitionsbetrag abziehen und das Ergebnis durch den Investitionsbetrag teilen.
Die folgende Wertetabelle soll Ihnen zeigen, was Sie hiermit anfangen können:
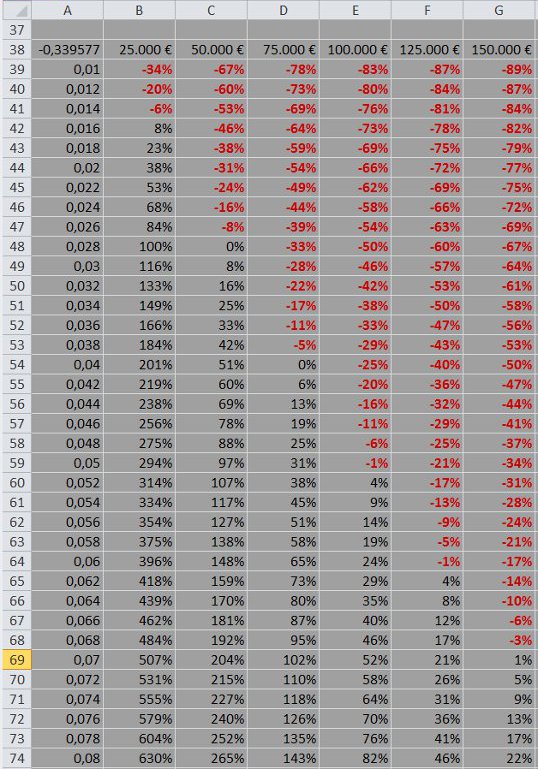
In Zelle A38 steht die Formel für den ROI =(XKAPITALWERT(E4; G7:G34; A7:A34) -XKAPITALWERT(E4; D7:D34; A7:A34) -E1)/E1. Sie können diesen Wert durch das benutzerdefinierte Format ;;; ausblenden.
Die Zellen B38 bis G38 enthalten unterschiedliche Investitionsbeträge.
In Spalte A sehen Sie mögliche Erhöhungen der Kundenbindungsrate. Derartige Zahlenreihen können Sie durch den Dialog Start / Füllbereich / Reihe erzeugen.
Die Wertetabelle erhalten Sie, indem Sie den Bereich A38:G74 mit der Maus markieren, den Dialog Daten / Was-wäre-wenn-Analyse / Datentabelle wählen, in das Feld »Werte aus Zeile« E1 eintragen, in das Feld »Werte aus Spalte« E2 schreiben und OK wählen.
Negative ROI-Werte habe ich rot gefärbt (Dialog Start / Bedingte Formatierung / Neue Formel zur Ermittlung der zu formatierenden Zellen verwenden).
Wenn Sie 25.000 Euro investieren und die Kundenbindungsrate hierdurch um 1,6 Prozentpunkte erhöht wird, so erreichen Sie für dieses Projekt einen ROI in Höhe von 8 Prozent.
Sie sehen anhand der Tabelle, dass die Einführung eines Kundenbindungsmanagements unrentabel sein kann.
Sie fordern zum Beispiel eine Mindestverzinsung von 13 Prozent und ziehen in Betracht, 150.000 Euro zu investieren. Auf Basis der obigen Daten müssten Sie durch Ihr neues Kundenbindungsmanagement in der Lage sein, Ihre Kundenbindungsrate um mindestens 7,6 Prozentpunkte zu erhöhen.
Fazit
Die Kundenbindungsrate hat einen sehr starken Einfluss auf den Gewinn, den Sie mit der betreffenden Kundengruppe erzielen.
Investitionen zur Erhöhung der Kundenbindungsrate können trotzdem unrentabel sein; es kommt nicht nur auf die zusätzlichen Erträge an (Erhöhung des Kundenwerts), sondern auch auf die hierfür erforderlichen Aufwendungen.
Die Beispieldaten legen nahe, dass relativ kleine Investitionen in die Kundenbindung leicht zu rechtfertigen sind.
Für hohe Investitionen in die Kundenbindung empfehle ich eine Was-wäre-wenn-Analyse mit Excel, mit der Sie einschätzen können, unter welchen Bedingungen Sie die von Ihnen geforderte Mindestverzinsung erreichen.
Internetseiten
Fachbeiträge
Das liberale Propaganda-Handbuch, Taschenbuch, 382 Seiten
Einführung in die Statistik-Software R Commander
Business Cases für den Verkauf
Fachliteratur suchen mit Google Scholar, WorldCat etc. pp.
Ghostwriter für Dissertationen, Bachelor- und Masterarbeiten
Wissenschaftliches Ghostwriting
Content-Marketing mit White Papers für Start-up-Unternehmen im B2B-Geschäft
1. White Papers als Werbemittel
2. Fallstudien im Sinne von White Papers
Warum White Papers im B2B-Geschäft häufig wirkungsvoller sind als klassische Werbung
Lead-Management im B2B-Geschäft - warum und wie?
White Papers erstellen - von der Themenwahl bis zum Layout