Ghostwriting-Service Dr. Rainer Hastedt
Erfolgsmessung im Marketing - Folge 18: Regressionsanalysen (Marketing-Mix-Modellierung)
Zum Marketing Mix gehören alle Variablen, die den Absatz eines Unternehmens beeinflussen und von diesem Unternehmen als Steuergrößen angesehen werden können.
Der Marketing Mix eines Unternehmens umfasst normalerweise Variablen aus vier Kategorien: Produkt (physische Eigenschaften, Technologie, Qualität, Sortiment), Preis (Listenpreise, Sonderangebote, Rabatte), Promotion (Werbung, Verkaufsförderung) und Place (Distribution, Verfügbarkeit).
Mit Regressionsanalysen können Sie untersuchen, wie sich bestimmte Änderungen im Marketing Mix auf das Ergebnis Ihres Unternehmens auswirken.
Sie erhalten durch diese Art der Marketing-Mix-Modellierung Antworten auf drei Arten von Fragen:
- Wie stark beeinflussen einzelne Variablen Ihr Ergebnis? Sind bestimmte Marketing-Mix-Variablen wirkungsvoller als andere?
- Wie würde sich Ihr Ergebnis ändern, wenn Sie eine Marketing-Mix-Variable auf einem neuen Niveau festsetzen?
- Wie viel sollten Sie für bestimmte Marketing-Mix-Variablen aufwenden, zum Beispiel für Werbung oder Preisnachlässe?
Die Marketing-Mix-Modellierung ist in konzeptioneller Hinsicht relativ leicht, weil Sie hierfür auf eine umfangreiche Fachliteratur zurückgreifen können.
Das Hauptproblem der Marketing-Mix-Modellierung liegt normalerweise in der Datenbeschaffung. Sie müssen unter Umständen mit Hilfsgrößen arbeiten, die zum Beispiel das Verhalten Ihrer Konkurrenten oder die Marktentwicklung operationalisieren, Variablen durch einen Index messen oder Ihre Daten bereinigen. Ein wichtiger Aspekt ist auch die Wahl der Zeiteinteilung (zum Beispiel Wochen- oder Monatswerte), weil hiervon die späteren Ergebnisse abhängen.
Die Marketing-Mix-Modellierung eignet sich vor allem für Unternehmen mit relativ vielen Kunden, von denen jeder einzelne nur wenig ins Gewicht fällt.
Ich werde die Marketing-Mix-Modellierung anhand eines Zahlenbeispiels erläutern, in dem ich das optimale Werbebudget berechne.
Meine Zeitreihen
Sie sehen meine Daten in der folgenden Excel-Tabelle:
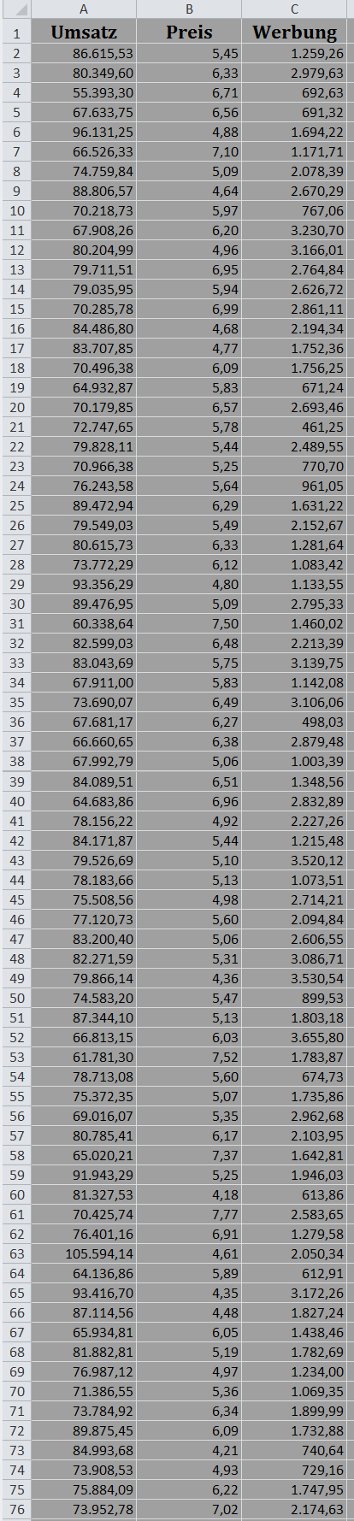
Spalte A enthält die letzten Monatsumsätze eines Fastfood-Restaurants. Es kann sein, dass diese Zeiteinteilung zu grob ist (siehe zum Beispiel Gerard J. Tellis und Philip Hans Franses: Optimal Data Interval for Estimating Advertising Response, Marketing Science, Jahrgang 25, 2006, Nr. 3, Seite 217-229).
Spalte B enthält den im jeweiligen Monat geltenden Preis, der durch einen Preisindex gemessen wurde (gewichteter Durchschnittswert aus den Preisen der verkauften Speisen und Getränke).
Spalte C enthält die monatlichen Aufwendungen für Werbung. Hierbei nehme ich an, dass die Werbung von gleichbleibender Qualität ist. Das Restaurant verteilt zum Beispiel in einem Monat weniger Flyer als in einem anderen.
Ich habe meine Daten so zusammengestellt, dass keine Schätzprobleme auftreten und ich alle Berechnungen mit Excel durchführen kann.
Meine Regressionsgleichung
Als Ausgangspunkt dient die folgende Regressionsgleichung:
Umsatz t = β0 + β1* Preis t + β2* Werbung t + β3* (Werbung t)2 + e t mit
t = 1, ..., 75
Der Koeffizient β1 misst den Einfluss des Preises auf den Umsatz. Ein negativer Wert (β1< 0) bedeutet, dass eine Preiserhöhung den Umsatz mindert, sofern alles andere gleich bleibt.
Der Ausdruck β2* Werbung t + β3* (Werbung t)2 beziffert den Einfluss der Werbung auf den Umsatz. Im Fall β2> 0 und β3< 0 wird die Umsatzwirkung der Werbung mit zunehmendem Einsatz sukzessive kleiner, sofern alles andere gleich bleibt.
Ich habe die Regressionsgleichung mit einem meiner Excel-Templates geschätzt und geprüft (Irrtumswahrscheinlichkeit α = 0,05):
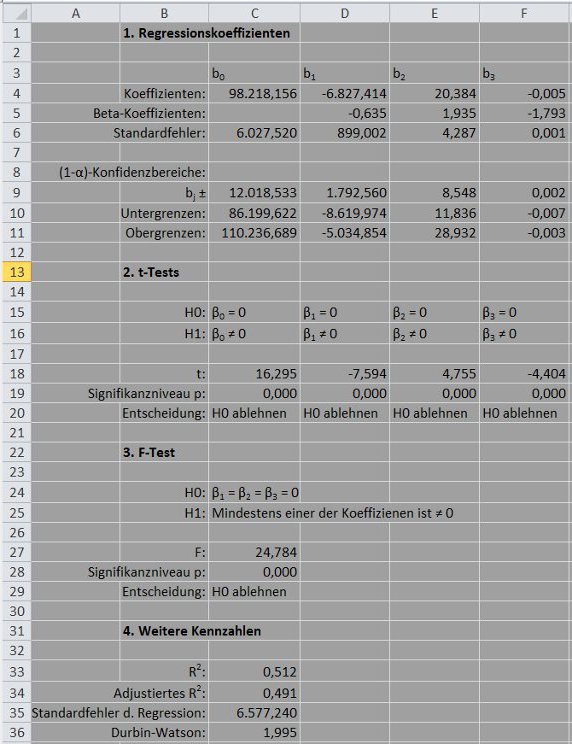
Außerdem habe ich mir über den Dialog Daten / Datenanalyse / Regression die Residuenplots ausgeben lassen.
Nach der obigen Excel-Tabelle sind alle vier Koeffizienten statistisch signifikant. Jeder Schätzwert hat das erwartete Vorzeichen. Anzeichen für Autokorrelation oder Heteroskedastizität fehlen (Durbin-Watson-Koeffizient bei zwei, Residuenplots ohne auffällige Muster).
Die gewählte Regressionsgleichung und die Schätzergebnisse sind somit akzeptabel.
Ich berechne jetzt das optimale Werbebudget. Hierzu betrachte ich den Gewinn als Funktion der Variablen Werbung und bilde die erste Ableitung.
Gewinn = Umsatz - Kosten
Der Umsatz ergibt sich durch Einsetzen der Schätzwerte in meine Regressionsgleichung. Für eine beliebige Periode t gilt somit:
Umsatz = 98,218-6.827,414*Preis+20,384*Werbung-0,005*Werbung2
Ich differenziere diese Gleichung nach der Variablen Werbung und erhalte:
Umsatz' = 20,384-2*0,005*Werbung
Wenn ich die Aufwendungen für Werbung um eine Einheit erhöhe und alles andere gleich bleibt, dann steigen meine Kosten um mehr als eine Einheit, weil ich die geforderte Mindestverzinsung r berücksichtigen muss. Im Fall von Monatswerten gilt somit für die Grenzkosten:
Kosten' = 1 + r* mit r* = r/12
Die Gleichung für den Grenzgewinn lautet demnach:
Gewinn' = 20,384-2*0,005*Werbung - 1 - r*
Ich setze die erste Ableitung gleich Null und erhalte bei einer Mindestverzinsung von r = 10% (r* = 0,1/12) für die Variable Werbung den Wert 2.051,50 Euro. Weil Gewinn'' negativ ist, handelt es sich hierbei um ein Maximum.
Beachten Sie bitte, dass die aus der obigen Excel-Tabelle übernommenen Zahlen 20,384 und 0,005 mit dem Dialog »Zellen formatieren« gerundet sind. Excel hat bei der Berechnung des Maximalwerts anstelle von 20,384 und 0,005 die Werte 20,3839334003373 und 0,00472229672039121 verwendet.
Ergebnis:
In den Monaten t = 1 bis 75 (Zellen C2 bis C76) betrugen die durchschnittlichen Aufwendungen für Werbung 1.867,64 Euro.
Das optimale Niveau in Höhe von 2.051,50 Euro liegt deutlich höher.
Alternative Regressionsgleichungen
Ich beschäftige mich jetzt mit der Frage, ob ich die im letzten Abschnitt verwendete Regressionsgleichung vereinfachen kann.
1. Versuch
Ich verwende die folgende Regressionsgleichung:
Umsatz t = β0 + β1* Preis t + β2* Werbung t + e t mit t = 1, ..., 75
Mit dieser Gleichung wird unterstellt, dass der mit einer sukzessiven Ausweitung des Werbebudgets erzielte Umsatzzuwachs konstant bleibt.
Excel liefert die folgenden Ergebnisse:
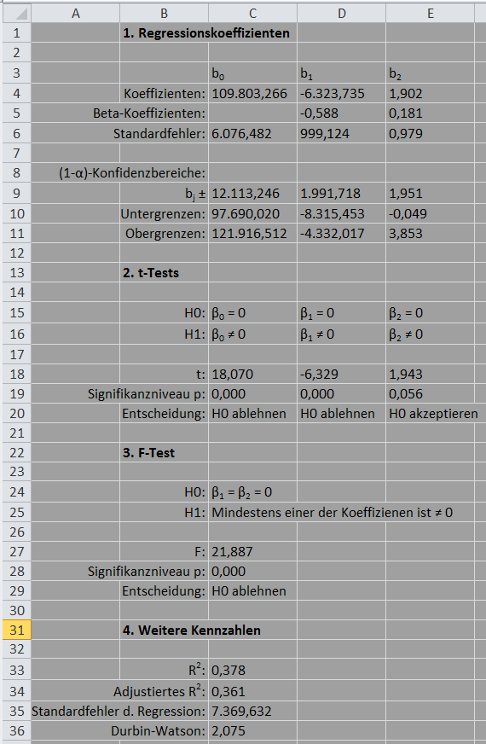
Die Variable Werbung hat jetzt keinen signifikanten Einfluss auf den Umsatz (Zelle E15 bis E20). Das durch die zweite Regressionsgleichung beschriebene Regressionsmodell ist somit inakzeptabel.
2. Versuch
Ich verwende die folgende Regressionsgleichung:
Umsatz t = β0 + β1* Werbung t + β2* (Werbung t)2 + e t mit t = 1, ..., 75
Diese Gleichung ist interessant, weil das von mir ermittelte optimale Werbebudget nicht von der Variablen Preis abhängt. Es könnte sein, dass die Variable Preis überflüssig ist.
Excel liefert die folgenden Ergebnisse:
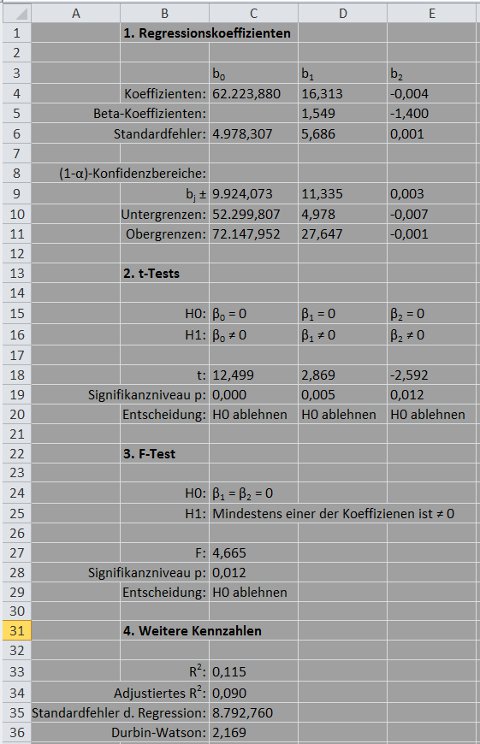
Bei dieser Gleichung sind alle drei Koeffizienten statistisch signifikant. Das Weglassen der Variablen Preis macht sich vor allem durch das extrem niedrige Bestimmtheitsmaß (Zelle C33 und C34) bemerkbar.
Ich halte das Weglassen der Variablen Preis daher für inakzeptabel.
Wenn ich trotzdem mit der Regressionsgleichung Umsatz t = β0 + β1* Werbung t + β2* (Werbung t)2 + e t arbeite, so erhalte ich ein optimales Werbebudget in Höhe von 2.075,91 Euro.
Mit der wesentlich besseren Regressionsgleichung Umsatz t = β0 + β1* Preis t + β2* Werbung t + β3* (Werbung t)2 + e t ergab sich ein Wert in Höhe von 2.051,50 Euro.
Ein relativ schlechtes Modell muss nicht unbedingt zu falschen Einschätzungen führen.
Internetseiten
Fachbeiträge
Das liberale Propaganda-Handbuch, Taschenbuch, 382 Seiten
Einführung in die Statistik-Software R Commander
Business Cases für den Verkauf
Fachliteratur suchen mit Google Scholar, WorldCat etc. pp.
Ghostwriter für Dissertationen, Bachelor- und Masterarbeiten
Wissenschaftliches Ghostwriting
Content-Marketing mit White Papers für Start-up-Unternehmen im B2B-Geschäft
1. White Papers als Werbemittel
2. Fallstudien im Sinne von White Papers
Warum White Papers im B2B-Geschäft häufig wirkungsvoller sind als klassische Werbung
Lead-Management im B2B-Geschäft - warum und wie?
White Papers erstellen - von der Themenwahl bis zum Layout